
《实验力学》

进行结构设计,首先要掌握材料的力学性能。历史上,达芬奇 (1452-1519) 很可能是利用试验方法测定材料力学性能的第一人。作为画家,在他完成的作品之后通常要悬挂起来供人们欣赏,而挂画的铁丝时常会发生断裂的现象,由此达芬奇设计过测量铁丝断裂强度的实验装置,并开展了相应的研究。
图2 伽利略和他的拉伸强度、弯曲强度试验[1]
不过,达芬奇和伽利略的试验只能称之为结构强度试验,还不能称之为材料强度试验,他们的试验结果很强的依赖于结构形式。
到了19世纪上半叶,链式悬索桥在欧美国家兴起,然而,由于缺乏桥梁结构力学、以及材料性能方面的知识,时常出现桥梁倒塌事故。此外,工业革命的到来使得锅炉成了工业生产中的常见设备,然而,锅炉爆炸事故却如同家常便饭,时常会发生灾难性的爆炸事故。1850年位于曼哈顿的一家机械车间发生锅炉爆炸,共造成60多人丧生。人们迫切的需要掌握各种材料的力学性能,工程师们时常抱怨缺乏安全可靠的材料性能参数而难以进行合理设计。当时美国《工程杂志》 (Engineering Magazine) 的主编 Van Nostrand 曾描述这一状况时说(大意):人们对材料的知识的认知目前绝对是经验性的,在使用新材料或旧材料以新形式使用之前,唯一安全的方法是进行实验。
1800年前后,人们设计了许多各式各样的材料试验机。其中较有代表性的是 Eytelwein 设计的一款材料拉伸试验机,如图3所示。该试验机采用了杠杆式设计,为便于固定试样,试样设计为“棒骨”状,然后利用杠杆原理对材料施加载荷,通过砝码距离悬挂点的距离,可以轻松的换算出施加在试样 HK 上的载荷大小。理论上,只要杠杆有足够的大,就可以提供足够大的拉力。不过 Eytelwein 的实验装置只能测定材料的极限强度,还不能测试材料的屈服极限、弹性模量等指标。
Gerstner的试验装置如图5所示,起初用来测定钢琴线在受拉条件下的力与变形。该实验装置将试样安装在图中mn处,AB 为一长杠杆,C 为杠杆支点,CA长4.73m,CB 杆加配重后可保持杠杆平衡,H 为配重,通过H 的位置可换算出m 点施加的力的大小。m 点在C 点偏右一点,并在C 点设置一个传动装置,通过旋转滚子可改变杠杆的倾斜程度,同时带动钢琴线被拉紧或放松。当扭动旋钮时,长杆mA 发生上下倾斜,m 处很小的位移在A 端被放大(该装置可放大到54倍),AD 为竖直放置的标有刻度的标尺,读出A 点位移就可以换算出m 点的位移,进而获得钢琴线的变形量。
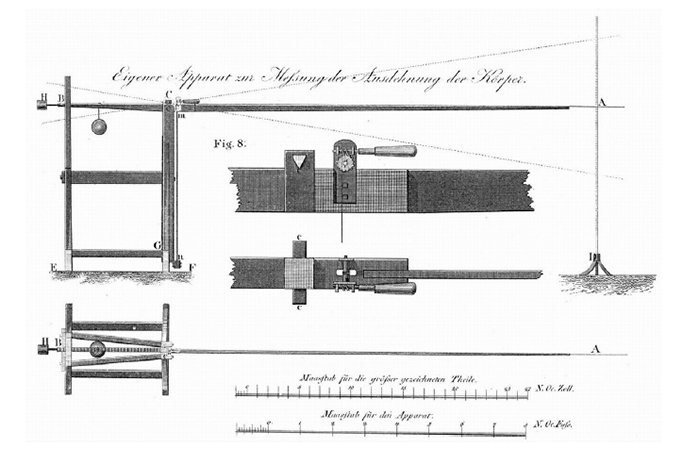
图5 Gerstner测量铁丝拉伸状态“力-变形”的实验装置[2]
借助于该试验装置,Gerstner 开展了一系列的钢琴线的拉伸试验,并使用多项式方法得出了铁线的抛物线形和无量纲力变形定律。
上式中,Fmax 和△lmax 是待定常数,F 和△l 是试验中的过程量。根据上式,可以绘制出力-变形曲线,如图6所示。

图6 依据Gerstner实验绘制的“力-变形”曲线[2]
Gerstner 对钢琴线、普通铁丝、钢发条等进行了10个不同的系列试验,发现实验与计算之间只有很小的偏差。此外,当 (△l/△lmax) 较小时,上式将可以认为满足线性关系,并区分了材料的弹性变形和塑性变形,以及加工硬化现象。他曾建议桥梁工程师们应用加工硬化来提高链条强度,而不是“为获得足够的安全性,铁杆仅应承受一半的破坏载荷”。
尽管Gerstner 的实验装置可以同时测定力与变形,但由于他选择多项式函数式(上式)来描述力与变形的关系,还不足以清晰的区分屈服强度。有关屈服强度,人们在法国科学家Jean-Victor Poncelet 的《关于在梅斯中进行实验以研究金属线中延伸电阻的注意事项》(Note sur les Expériences à Metz pour étudier la résistance de l'extension dans le fils métalliques) 报告中发现了一张铁材料的力与变形曲线,如图7所示,图中不仅清楚地展示了胡克定律的范围和屈服强度,而且写出了弹性模量,只是没有标注出尺寸。
上一篇:中国矿业大学材料力学实验报告
下一篇:没有了